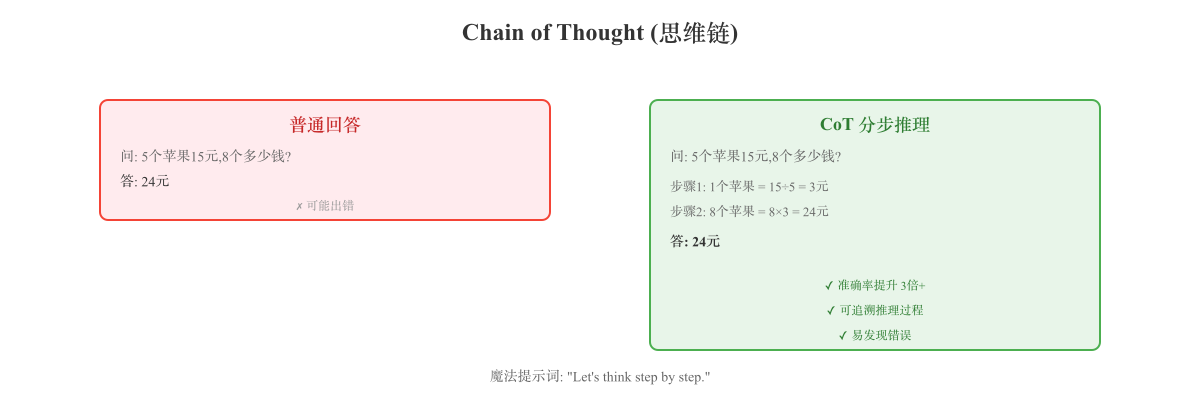
什么是 Chain of Thought（思维链）#

实际例子：

例子 1：数学题

问题："如果 5 个苹果卖 15 元，8 个苹果多少钱？"

普通 AI（可能错）：

CoT AI（分步骤）：

例子 2：逻辑推理

问题："张三比李四大 3 岁，李四比王五小 2 岁，王五 20 岁，张三多大？"

CoT 推理：

例子 3：常识推理

问题："我把袜子放进烘干机，现在湿袜子在哪？"

CoT 推理：

两种使用方式：

方式 1：Zero-shot CoT（零样本）

只需要在提示词最后加："Let's think step by step"（让我们一步步思考）

方式 2：Few-shot CoT（少样本）

给 AI 几个"有步骤"的例子，让它学会这个模式。

AI 会模仿例子的格式，给出步骤化的答案。

为什么有效？

传统 AI 的问题：

• 复杂问题"一步到位"容易出错
• 就像让小学生直接心算 237 × 48，很难算对

CoT 的优势：

• 把复杂问题分解成简单步骤
• 每步都简单，串起来就能解决复杂问题
• 就像"分步计算"，降低出错率

数学原理：

适用场景：

✅ 特别有效：

• 数学题（尤其是多步骤）
• 逻辑推理（"谁比谁大"这类）
• 常识推理（需要多步思考）
• 代码调试（一步步排查）

❌ 不太需要：

• 简单问答（"秦始皇哪年统一六国？"）
• 翻译（不需要推理）
• 总结文章（直接提取即可）

实际使用：

在 ChatGPT 中：

在代码中：

# OpenAI API
response = openai.chat.completions.create(
    model="gpt-4",
    messages=[
        {"role": "system", "content": "解决问题时，请一步步列出推理过程。"},
        {"role": "user", "content": "鸡兔同笼，35 个头，94 只脚，多少只鸡？"}
    ]
)

进阶技巧：

1. Self-Consistency（自洽性）

让 AI 多次推理，选最常见的答案：

2. Tree of Thoughts（思维树）

不只一条推理链，探索多条路径：

3. Program of Thoughts（程序化思维）

把推理步骤转成代码执行：

常见误区：

误区 1："CoT 是万能的"

• 不对！简单问题用 CoT 反而浪费 token
• 只在复杂推理时用

误区 2："一定要用英文'Let's think step by step'"

• 不一定！中文"让我们一步步思考"也行
• 关键是让 AI 明白"要分步骤"

误区 3："CoT 一定更准"

• 不一定！如果 AI 的每一步都错，最后还是错
• CoT 只是"降低出错率"，不是"保证正确"

实际效果：

研究数据（Google 论文）：

• 数学题准确率：17% → 58%（提升 3.4 倍！）
• 逻辑推理：29% → 79%（提升 2.7 倍）
• 常识推理：47% → 74%（提升 1.6 倍）

#说白了，Chain of Thought 就是让 AI "把解题步骤写出来"——通过分步推理，把复杂问题拆成简单小问题，大幅提升准确率。就像老师说的："不要直接写答案，要列出解题过程！"

Chain of Thought（CoT，思维链）是一种提示工程技术，通过引导大型语言模型（LLM）逐步展示推理过程，而不是直接给出答案，从而显著提升复杂推理任务的准确性。

#核心概念

#传统推理 vs CoT 推理

传统推理（Direct Answer）：

CoT 推理（Step-by-step）：

关键差异：

• 传统：问题 → 答案（黑盒）
• CoT：问题 → 推理步骤 → 答案（透明）

#为什么有效？

核心原理：

1. 分解复杂性：将复杂问题拆解为简单子问题
2. 降低单步错误率：每一步都相对简单，容易做对
3. 可解释性：能看到推理过程，发现错误

数学直觉：

#CoT 的两种形式

#1. Few-shot CoT（少样本思维链）

通过在提示词中提供带推理步骤的示例，让模型学习这种模式。

示例：

模型输出：

#2. Zero-shot CoT（零样本思维链）

无需示例，只需在提示词末尾添加魔法短语：

"Let's think step by step."（让我们一步步思考）

示例：

模型输出：

为什么有效？

• "Let's think step by step" 触发了模型的推理模式
• 模型在预训练时见过大量"分步骤解题"的文本
• 这个短语激活了相关的推理模式

其他有效的魔法短语：

• "Let's solve this problem step by step."
• "Let's break this down:"
• "让我们一步步分析："
• "让我逐步思考："

#实际应用案例

#案例 1：数学应用题

问题：

Zero-shot CoT：

#案例 2：逻辑推理

问题：

CoT 推理：

#案例 3：常识推理

问题：

CoT 推理：

#案例 4：代码调试

问题：

def calculate_average(numbers):
    total = 0
    for num in numbers:
        total += num
    return total / len(numbers)

# 调用
result = calculate_average([])
# 错误：ZeroDivisionError

CoT 调试：

#CoT 的变体和扩展

#1. Self-Consistency CoT（自洽性思维链）

思想： 多次生成推理路径，选择最常见的答案。

流程：

优点：

• 提高准确性（通过"多数投票"）
• 减少单次推理错误的影响

缺点：

• 成本增加（需要多次 LLM 调用）
• 速度变慢

#2. Tree of Thoughts（思维树，ToT）

思想： 探索多个推理路径，像搜索树一样。

示例： 用 4 个 4 算出 24

代表模型：

• GPT-4 with ToT
• Claude with ToT

#3. Program of Thoughts（思维程序，PoT）

思想： 将推理步骤转换为可执行代码。

示例：

问题： "1 到 100 之间有多少个质数？"

CoT（纯文本推理）：

PoT（程序化推理）：

# 生成代码
def count_primes(n):
    count = 0
    for num in range(2, n + 1):
        is_prime = True
        for i in range(2, int(num**0.5) + 1):
            if num % i == 0:
                is_prime = False
                break
        if is_prime:
            count += 1
    return count

result = count_primes(100)
print(result)  # 25

优点：

• 复杂计算交给代码（更准确）
• 适合数学、数据分析任务

#4. Least-to-Most Prompting（从简到难）

思想： 先解决简单子问题，再组合成复杂问题的答案。

示例：

问题： "最后一个字母是元音字母的单词连接起来：take the last letters of the words in 'Elon Musk' and concatenate them."

Least-to-Most：

#实践建议

#1. 何时使用 CoT

✅ 推荐场景：

• 多步骤数学题
• 逻辑推理
• 需要分析的问题
• 复杂的代码调试

❌ 不必要场景：

• 简单事实查询（"秦始皇哪年统一六国？"）
• 翻译
• 总结
• 简单计算（"1+1=?"）

#2. 提示词模板

Zero-shot CoT 模板：

Few-shot CoT 模板：

中文 Zero-shot CoT：

#3. API 调用示例

OpenAI GPT-4：

import openai

response = openai.chat.completions.create(
    model="gpt-4",
    messages=[
        {
            "role": "system",
            "content": "解决问题时，请逐步展示你的推理过程。"
        },
        {
            "role": "user",
            "content": "如果 3 个苹果卖 9 元，8 个苹果多少钱？\n\nLet's think step by step."
        }
    ],
    temperature=0  # 确定性输出
)

print(response.choices[0].message.content)

Anthropic Claude：

import anthropic

client = anthropic.Client(api_key="...")
response = client.messages.create(
    model="claude-3-5-sonnet-20241022",
    messages=[{
        "role": "user",
        "content": "问题：鸡兔同笼，35 个头，94 只脚，多少只鸡？\n\n请一步步推理。"
    }],
    max_tokens=1024
)

print(response.content[0].text)

#性能提升数据

#学术研究成果（Google Brain，2022）

#模型规模影响

结论： CoT 在大模型（> 100B 参数）上效果最佳。

#常见问题

Q: 为什么小模型用 CoT 效果不好？

A:

• 小模型（< 10B）缺乏足够的推理能力
• 即使"列步骤"，每一步都可能出错
• 建议：至少 70B+ 参数模型

Q: CoT 会增加多少成本？

A:

• 输出 token 数通常增加 2-5 倍
• 例如：原本 20 token → CoT 后 50-100 token
• 成本相应增加

Q: 中文和英文 CoT 效果一样吗？

A:

• 英文效果稍好（训练数据更多）
• 但中文 CoT 也很有效
• 建议：中文任务用中文提示词

Q: 如何验证 CoT 的推理是否正确？

A:

• 阅读推理步骤（人工检查）
• 使用 Self-Consistency（多次生成，投票）
• 对于数学题，可以用代码验证答案

#参考资料

• Chain-of-Thought Prompting Elicits Reasoning in Large Language Models - CoT 原始论文（Google Brain）
• Large Language Models are Zero-Shot Reasoners - Zero-shot CoT 论文
• Self-Consistency Improves Chain of Thought Reasoning - Self-Consistency CoT
• Tree of Thoughts: Deliberate Problem Solving with Large Language Models - ToT 论文
• Program of Thoughts Prompting - PoT 论文
• 什么是 Few-shot 和 Zero-shot Learning - 本站相关文章