什么是拟合与过拟合？#

(图片来自 arockialiborious.com)

拟合（Fitting）是机器学习中让数学模型贴合观测数据的过程。就像根据身材定制衣服，好的拟合需要平衡贴合度（Goodness of Fit）与泛化能力（Generalization）：

• 贴合度：模型对训练数据的解释能力（如衣服的合身程度）
• 泛化能力：模型对新数据的预测能力（如衣服对不同体型的适应性）
• 平衡艺术：完美贴合训练数据 ≈ 100%定制服装，但可能无法适应新体型

#拟合的本质

预计阅读时间: 4 分钟

• 数学定义：寻找函数 $f(x)$ 使得 $f(x_i) \approx y_i$（$i=1,...,n$）
• 核心矛盾：模型容量与数据复杂度
• 关键指标：训练误差（Training Error） vs 测试误差（Test Error） vs 验证误差（Validation Error）

#欠拟合：当模型不够聪明

欠拟合（Underfitting）是模型无法捕捉数据基本模式的现象：

• 典型特征：训练误差和测试误差都较高
• 危险信号：模型忽略明显的数据趋势
• 经典案例：用线性模型拟合正弦波数据

#过拟合：当聪明反被聪明误

过拟合（Overfitting）是模型完美记忆训练数据却失去泛化能力的现象：

• 典型特征：训练误差趋近于0，测试误差突然上升
• 危险信号：模型开始拟合噪声和异常值
• 经典案例：用10次多项式拟合10个数据点

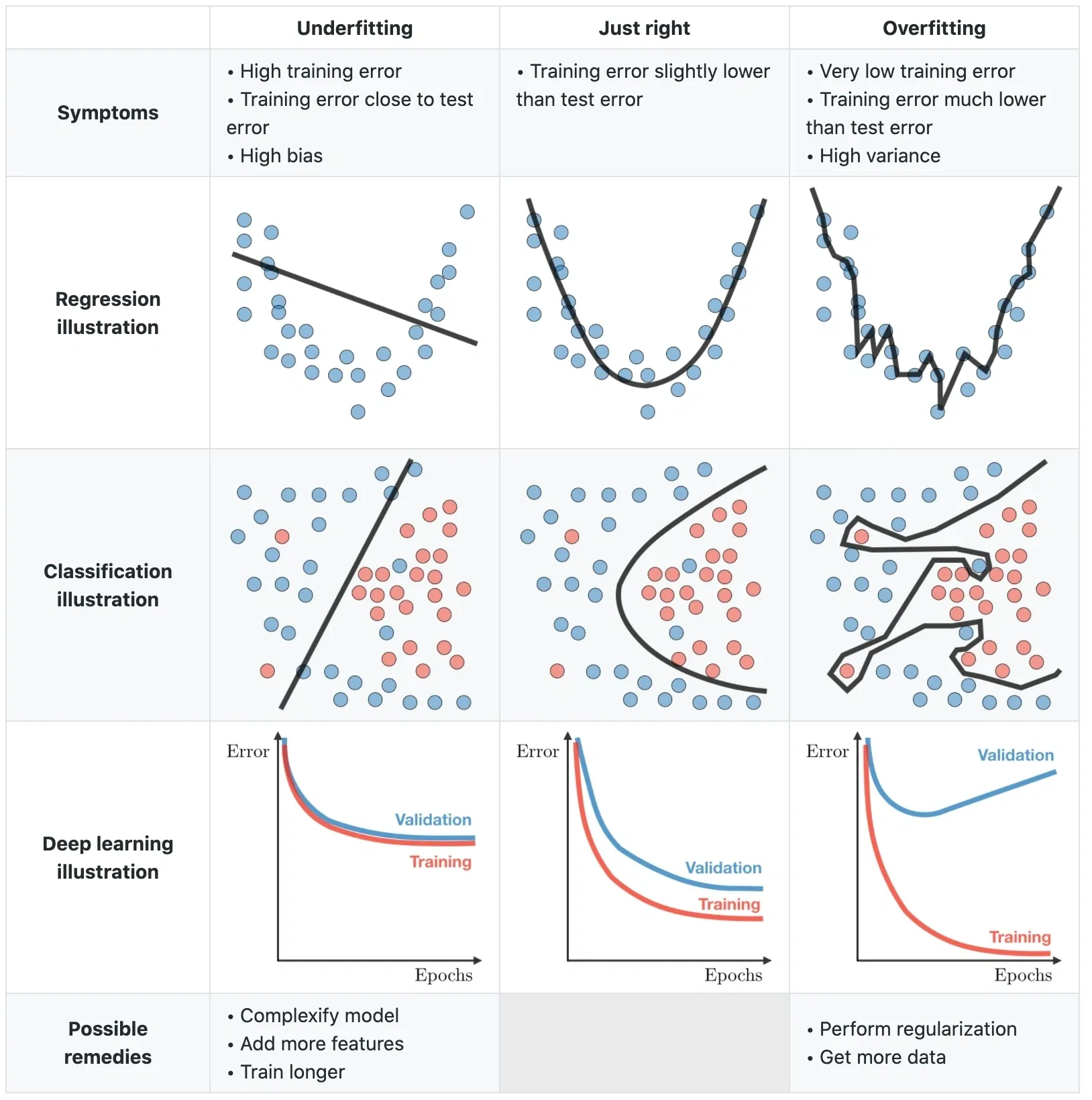
#拟合程度对比表

特征	欠拟合	适度拟合	过拟合
模型复杂度	过低	匹配数据复杂度	过高
训练误差	高	低	趋近于0
测试误差	高	低	突然升高
数据利用效率	浪费信息	有效提取模式	记忆噪声
典型解决方法	增加模型复杂度	——	正则化/早停/数据增强

#数学视角

#1. 优化目标

给定数据集 $(X,y)$，拟合过程可表示为： $\min_{\theta} \frac{1}{n}\sum_{i=1}^n L(f_\theta(x_i), y_i) + \lambda R(\theta)$ 其中：

• $L$ 为损失函数（如MSE/交叉熵）
• $R(\theta)$ 为正则化项（L1/L2正则）
• $\lambda$ 为正则化系数

#2. 偏差-方差权衡

泛化误差可分解为： $\mathbb{E}[(y-\hat{f})^2] = \underbrace{(\mathbb{E}[\hat{f}] - f)^2}_{\text{Bias}^2} + \underbrace{\mathbb{E}[(\hat{f}-\mathbb{E}[\hat{f}])^2]}_{\text{Variance}} + \sigma^2$

• 高偏差：模型过于简单（欠拟合）
• 高方差：模型过于复杂（过拟合）
• 黄金平衡：通过调整模型复杂度找到最小总误差点

过拟合发生时，模型满足： $\mathbb{E}[L_{train}] \ll \mathbb{E}[L_{test}]$ 即训练误差显著小于测试误差。

#Refs

• Underfitting vs Overfitting
• Wikipedia: Overfitting